Construimos un circuito sumador digital de 2 bit utilizando agua en lugar de electricidad como fluido.
Introducción
Los sistemas digitales, en su interior, manejan toda la información (textos, números, imágenes, sonidos, vídeos, ...) en base a sólo dos estados posibles de información que comúnmente se representan con las cifras 0 y 1. Codificar números con sólo dos estados o cifras se conoce como utilizar la base 2 o el sistema de numeración binario. Emplear sólo dos estados para codificar números (y en última instancia todo se puede convertir en números), facilita mucho las cosas de cara a fabricar una máquina de cálculo, ya que podremos usar cualquier sistema físico que pueda tener dos estados, como por ejemplo un interruptor. Lo siguiente es la representación del número 5 en binario, aprovechando los dos estados posibles de la posición (estable) de un vaso. Imagina lo complicado que sería representar las 10 cifras del sistema decimal con un vaso:

Para construir una máquina que pueda manejar estados, nos interesa utilizar algún tipo de fluido. Habitualmente se utiliza la electricidad, pero nada impide que empleemos otra clase de fluidos como el aire o el agua. Las principales diferencias serán la velocidad y miniaturización que permitirán los distintos fluidos, siendo difícil de superar las que permite la electricidad, sobre todo gracias al invento del transistor que equivale a una válvula de estado sólido y de tamaño microscópico.
Pero para demostrar que conceptualmente no hay diferencia entre las distintas tecnologías, y que los fundamentos lógicos que se utilizan son idénticos entre las distintas tecnologías, vamos a construir un sencillo sumador digital de 2 bits con agua.
Puertas lógicas
Antes de llegar a definir nuestra máquina, tenemos que hablar de algunos componentes que vamos a utilizar. Se trata de unos operadores pertenecientes no a la aritmética como podríamos esperar (suma, resta, multiplicación, división), sino a una rama de las matemáticas llamada álgebra de Boole o booleana (en honor a su autor George Boole). Esta rama define las reglas de la lógica, es decir el campo de lo verdadero y lo falso (dos estados, ¿te suena?), y la utilizamos porque siguiendo una serie de reglas, podemos efectuar con ella también cálculos aritméticos.
Vamos a definir una puerta lógica en base a lo que llamamos su tabla de verdad, es decir la correspondencia entre una configuración posible de sus entradas con sus salidas. Aunque existen una gran cantidad de puertas lógicas, aquí vamos a ir al grano y sólo vamos a hablar de las que utilizaremos para construir el Water Computer. Son las siguientes.
Puerta OR
Esta puerta lógica tiene dos entradas y una salida que se activa cuando cualquiera de las dos entradas están activas. Simbólicamente la representaremos con el siguiente pictograma:

Su tabla de verdad es:
| a | b | c |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Puerta semisumador
La siguiente puerta lógica que utilizaremos, internamente está compuesta de otras más básicas que no vamos a estudiar (AND y XOR). Aquí vamos a analizarla definiendo su funcionamiento global. La puerta semisumador tiene dos entradas y dos salidas. La representaremos con el siguiente pictograma que además expresa cómo están conectadas las puertas básicas en su interior:

Su tabla de verdad en esta ocasión es:
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Si tenemos unas mínimas nociones de binario, vemos que en realidad esta puerta está sumando los bits A y B. Ofrece el resultado en forma del número binario compuesto por las salidas CS. Vamos a traducir la tabla anterior a decimal para que se vea más claro:
| A | B | Suma |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 2 |
Circuito sumador
Utilizando una combinación de las dos puertas lógicas descritas anteriormente, vamos a construir una máquina sumadora de números de 2 bit. La máquina completa construida con los componentes (las puertas lógicas) que hemos descrito anteriormente, tendría el siguiente esquema:
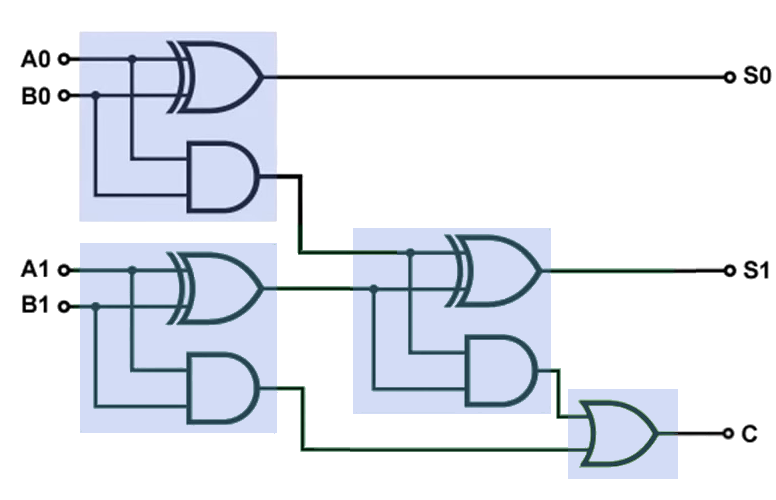
Celda hidráulica
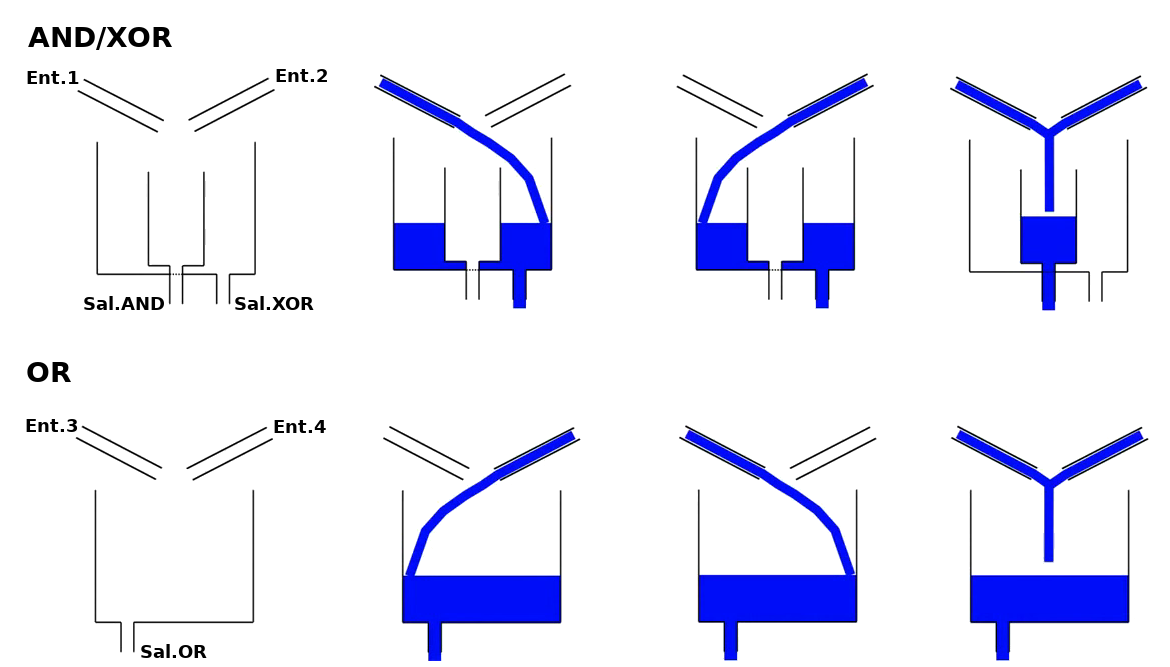
Como hemos comentado antes, sería muy sencillo implementar este sencillo circuito con electrónica (en concreto se utilizarían integrados de la familia 7400), pero nosotros vamos a realizar el circuito con tecnología hidráulica. En concreto el componente que nos va a permitir respetar las tablas de verdad de las puertas lógicas con agua va a ser la siguiente celda:
Según cómo la "cableemos", es decir dónde coloquemos las tuberías de entrada, la celda se comportará como una puerta OR o como una puerta semisumador. En la foto siguiente vemos las dos mitades de la celda y qué lado de la misma corresponde con una u otra puerta lógica. La diferencia entre ambas consiste únicamente en el pequeño vaso interior que hay en uno de los lados (en la foto el vaso se encuentra en la parte superior).

En el siguiente diagrama vemos el comportamiento del agua en la celda según se utilicen las entradas correspondientes a la puerta semisumador (1 y 2) o a la puerta OR (3 y 4):
Water Computer
Mostramos a continuación cómo se instalan las celdas en el Water Computer para que funcionen como puertas de uno u otro tipo.
 |
 |
| Puerta OR (vaso interior no utilizado) | Puerta semisumador (vaso interior utilizado) |
Completando el circuito que veíamos anteriormente con estas celdas, obtenemos lo que vamos a llamar el Procesador. Estamos acostumbrados a los ordenadores modernos que pueden modificar su comportamiento cambiando los programas que tienen en su interior. Los primeros ordenadores antiguos eran sólo máquinas de calcular, es decir, sólo sabían ejecutar un programa determinado que les venía "instalado" de fábrica y que de hecho estaba escrito a fuego por la combinación de sus puertas lógicas en el interior. Nuestro Water Computer se parece más a esas calculadoras iniciales que a un ordenador de hoy en día.

Además del procesador, el Water Computer tiene entrada y salida.
Empezamos hablando de la salida, lo que en un ordenador moderno normalmente se corresponde con la pantalla. En el Water Computer la salida son los tres tubos que se descuelgan por la parte inferior y que están rotulados con C, S1 y S0. Al igual que cuando estudiamos las celdas o puertas, la presencia de agua a la salida de uno de estos tubos indicará el valor Verdadero y la ausencia de agua el valor Falso. Como vamos a interpretar la salida como un número binario de 3 bits, Verdadero a la salida corresponderá con un dígito 1 y Falso con un dígito 0. Así si por ejemplo en un momento dado vemos que sale agua por las salidas C y S0 pero no por la S1, querrá decir que la salida está emitiendo el número binario 101, lo que en decimal como sabemos corresponde al número 5.
Las entradas típicas en un ordenador moderno son el teclado y el ratón. En el Water Computer la entrada son los cuatro tubos de la parte superior rotulados con B1, A1, B0 y A0. Al igual que la salida, vamos a interpretar la presencia de agua en los tubos como el valor lógico Verdadero que corresponderá con el dígito 1 binario y la ausencia de agua como el valor Falso que corresponderá con el 0 binario. Como sabemos, el procesador del Water Computer implementa un sumador de 2 bit, por lo que tenemos por un lado el número de dos bits A y por otro el B. Cada uno de ellos tendrá como máximo 2 dígitos en binario. A0 será el bit menos significativo del número A (el bit de la derecha) y A1 el más significativo (el bit de la izquierda). Por ejemplo si queremos introducir en el Water Computer el número 10 (2 en binario) como número A, por la entrada A1 tendrá que entrar agua y por la A0 no. Con el número B la situación es análoga pero en relación a las entradas B1 y B0. En nuestro Water Computer, hemos activado cada una de las cuatro entradas con unas pequeñas bombas de agua conectadas, una a cada entrada. Cuando queremos activar una entrada sólo tenemos que alimentar la bomba correspondiente. Esto mismo se podría hacer conectando las entradas a la red de agua de la casa e intercalando un pequeño grifo o válvula para controlar el flujo de agua y por lo tanto el estado de las entradas.
En el siguiente vídeo podemos ver el Water Computer sumando los números binarios siguientes:
- A = 10
- B = 11
El resultado como vemos es correcto:
- CS₁S₂ = 101
Human Computer
Para ilustrar la idea de que un circuito digital con puertas lógicas se puede implementar con cualquier elemento que respete las tablas de verdad, vamos a construir un Human Computer. En éste, las celdas OR y semisumador serán desempeñadas por personas. Para facilitar el "cableado" vamos a utilizar otra puerta lógica llamada "Buffer" que se comporta como un cable. Tiene una única entrada y una única salida que se limita a copiar el valor de la entrada. El símbolo en electrónica es:

Y su tabla de verdad es:
| a | b |
| 0 | 0 |
| 1 | 1 |
Ahora que conocemos el comportamiento de todas las puertas, sólo necesitamos 8 personas que memoricen las tablas de verdad de las puertas. El "reparto de la función" es el siguiente:
- Puerta OR: Azul. 1 persona. 2 entradas. 1 salida.
- Puerta semisumador: Rojo. 3 personas. 2 entradas. 2 salidas.
- Puerta buffer: Verde. 4 personas. 1 entrada. 1 salida.
Ya sólo queda componer el circuito con las 8 personas/puertas. Las entradas serán los hombros y las salidas las manos. En las entradas, un hombro tocado significa Verdadero y sin tocar Falso. En las salidas, activamos la salida tocando con la mano el hombro con que se encuentra conectada la salida, es decir tocar el hombro significa Verdadero y no tocarlo Falso. El circuito es el siguiente:

Haciendo este experimento, se hace muy evidente cómo la "velocidad de conmutación" de las puertas (en este caso, la agilidad con que las personas/puertas activan sus salidas cuando cambia el estado de las entradas) influye mucho en la velocidad de la máquina como conjunto. Los ordenadores electrónicos tienen el mismo problema. Por eso la miniaturización de los transistores que actúan como puertas, ha sido durante muchos años uno de los fundamentos por los que se ha conseguido aumentar la velocidad de cálculo, ya que cuanto más cerca están las puertas unas de otras, la información se propaga más rápido.


